几何压轴题, 考察的是迁移能力: 背后都有规律可循, 别怕

中考有一类几何压轴题，看起来挺难的，但摸透了背后规律，也没那么难。

这个规律是：考察的是学生的迁移能力，既然要“迁移”，前面的结论，后面肯定用得上。

下面我们来举例说明一下。

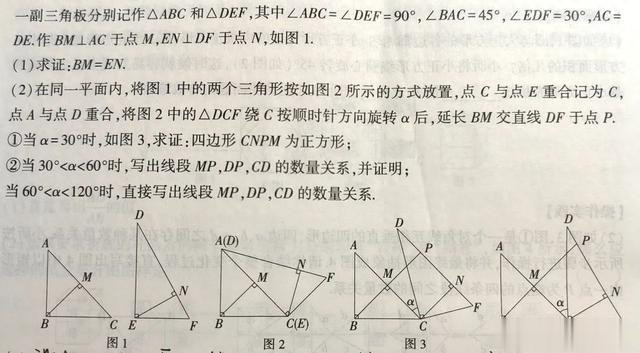
这两个三角形是我们熟悉的三角板。

看，这印证了我之前一篇文章的说法——这两个三角尺要焊死在脑子里。

从四年级开始，把这副三角尺焊死在脑子里！

好，话说回来。

看题目的第一问。

求证：BM＝EN。

不难做到，这是基础知识的考察，只要对45°、30°这两个特殊直角三角形足够熟悉就能够做出来。

第二问，开始旋转。

当α＝30度时，求证四边形CNPM是正方形——开始上难度了。

证明CNPM是矩形不难，关键是证明它的边相等。

这时候我们就要看上一问——记住：知识迁移，前面的结论后面能用。

前面的结论是什么？BM=EN，放到这里就是BM＝CN.

而我们又很容易想到BM＝MC＝CN，好了，得证。

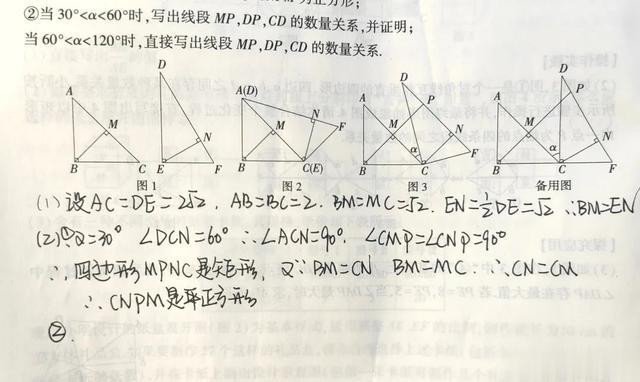
好，再往下看。

第三问，当30°＜α＜60°的时候，线段MP， DP，CD的关系。

什么关系？这几条线段根本不在一条线上，怎么比呢？

这时候要想到：前面的结论后面能用。

前面什么结论？正方形。

正方形四边相等，MP＝PN.

变形后，MP还等于PN吗？

从图片看是相等的——中考的时候要相信直觉，因为图很准确。

但我们作答时不能说【因为考官画的准确】，而要找证据。

之前我说过做辅助线的做法：取中、作平、连对角、延一倍。

做辅助线没灵感，记住这十个字：足以应对中考数学

在这里，四边形，我们连一连对角线PC呗。

一连就看出来了，有全等三角形。

接着思路打开了。

再往下走，当60°＜α＜120°时，这几条线段的数量关系。

有了前面的经验，我们很容易想：跟上面一样吗？

直觉上是一样，但我们要先把图画出来。

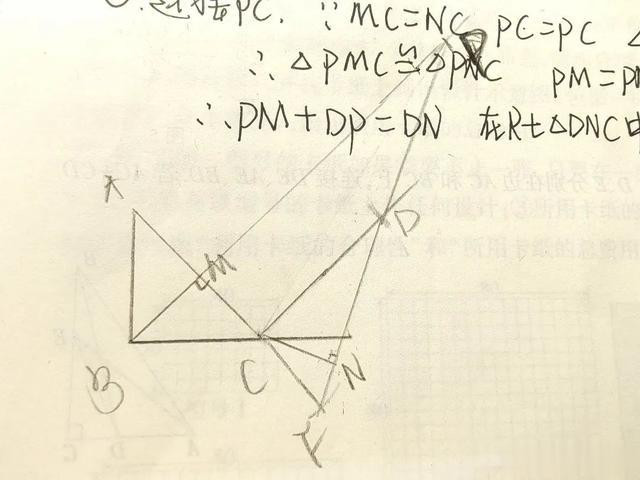
图画出来，就发现这次不是相加关系了。

我们说过：前一问的结论后面能用，其实不仅结论能用，做题方法也能用，现在我们用一用。

前面是怎么证明出来的？连接PC，照旧。

这下又明朗了。

好，题目做完了。

我们做一下总结：

几何压轴题不用怕，考察的是知识迁移能力；

既然是迁移，要记住前面的结论后面能用，前面的做题方法后面也能用；

做后面的题目时，想想前面的结论，前面的证明方法，对应到后面的问题中，基本就差不多了。

本文结束，谢谢阅读